Why I Force My Students to Prove That 1+1=1.

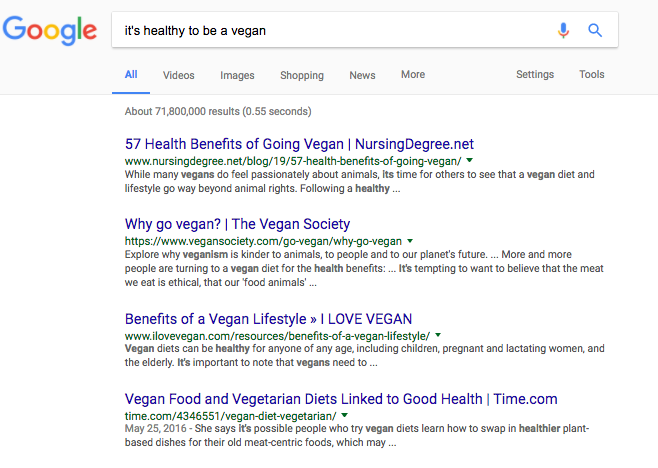
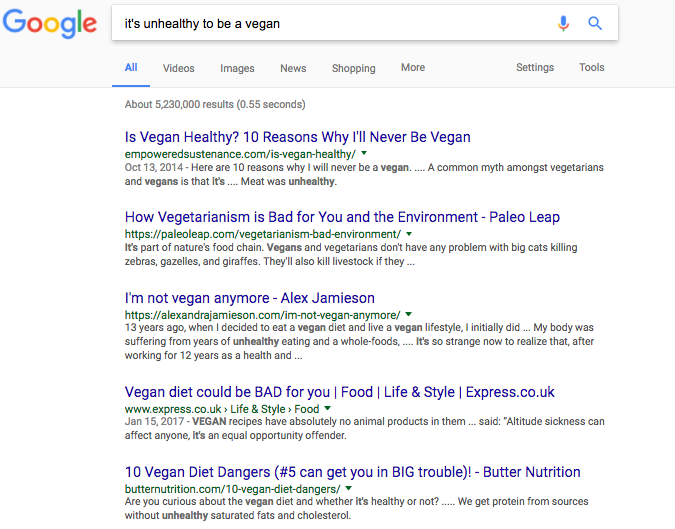
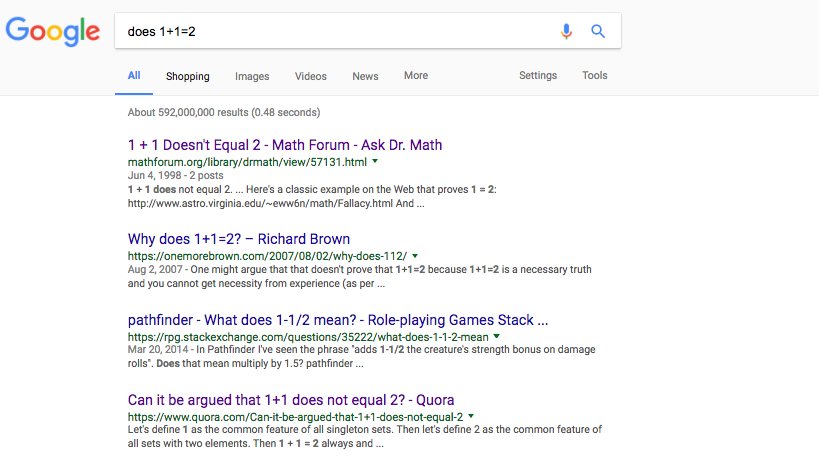
In the digital age, we are plagued by "fake news", hypersensitivity, and the anti-science movement. Skepticism is more important than ever.​

As a life coach, I help students develop curiosity, purpose, skills and interests that no one else has. After all, the road to success isn't paved with numbers (GPA, SAT, APs, etc.) -- it's paved with verbs! 

Which is why, last week, I asked one of my students to write a short paper about why it's healthy to be a vegan -- and​ a short paper about why it's unhealthy to be a vegan.

The takeaways were supposed to be:

1) Cool new information about nutrition, a topic she'd expressed interest in.
2) Learning about motivated reasoning. Regardless of the truth, you can Google anything and find evidence to support what you want to believe. 

Overall, the exercise was successful. There was one identical fact that appeared in both papers, but with completely opposite conclusions -- as well as "facts" that contradicted each other completely. One paper said vegans were healthy because they ate fewer artificial flavors and ingredients, and more fruits and vegetables. The other said vegans were unhealthy because their foods contain artificial ingredients, including "fake meat". 

I was like, "High five! You nailed it!"

But, I realized, veganism is complicated. It's not "yes healthy" or "no not healthy." There is legitimate, conflicting evidence on both sides. So I wanted to push the point further. 

"What is something you KNOW -- FOR SURE -- to be true?" I asked.

"Hmm... I know that 1+1=2."

"Are you sure? Google it."

Sure enough, two of the top four results indicated that 1+1 does NOT equal 2:

"That's your homework for next week," I told her. "Prove to me that 1+1 does NOT equal 2."

Yes, clearly she could just Google the proofs. That's fine. As long as, by next week, she could write out and explain every part of her proof to me, I don't care if she gets a little help from the Internet. 

"If you get stuck, or there are parts of the problem you don't understand, ask your math teacher for help," I continued. "It's a great way to get to know each other outside of the homework assignments -- and that's important, because she's going to be writing your recommendations next year."

(As I wrote in The Two Biggest Mistakes Students Make on Their College and High School Applications, top schools require amazing recommendations. If you can't prove that you engage deeply with your teachers, what's the point of admitting you to a school with world-class teachers and a great student:teacher ratio?)

Here's the proof she ended up using:

Let a = 1 and b = 1.

Therefore a = b, by substitution.

If two numbers are equal, then their squares are equal, too:

​a^2 = b^2

Now subtract b^2 from both sides:

a^2 - b^2 = 0

Now the left side of the equation is "the difference of two squares", and can be factored into:

(a-b)*(a+b) = 0

Since you have an equation, you can divide both sides by the same thing. So:

(a-b)*(a+b) / (a-b) = 0/(a-b)

On the left side, (a-b)/(a-b) simplifies to 1, and the right simplifies to 0. So:

1*(a+b) = 0

Since 1* X = X:

(a+b) = 0 

But a = 1 and b = 1, so...

1 + 1 = 0, or 2 = 0 

Divide both sides by 2, and you get:

1 = 0 

Add 1 to both sides, and:

1 + 1 = 1.
​
In fact, according to Math Forum, "You can prove that 47 = -3 or anything else you want. But of course you know that is wrong."

Why?

You can also "prove" that 1 = 2, that 2 = 1, and a host of other conclusions. Of course, each of these proofs has some small error in them (in the example, 0 was divided by  (a - b), and that can't happen)... but otherwise, everything checks out.

This matters, because we live in a world of fake news -- sometimes published be people with a political agenda (Hi, Russia!), sometimes pushed by people who are trying to make money (Hi, Gwyneth Paltrow!), sometimes frantically shared by people with strong emotions but little understanding of an issue (Hi, anti-vaxxers!). 

It's more important than ever to understand the importance of skepticism. 

Moreover, today's institutions of higher learning are rapidly coming to represent a smaller and smaller set of political and social values. According to psychologist Jonathan Haidt, today's college students are exposed to fewer and less provocative ideas than students of 2014. This isn't just bad from an educational standpoint. According to the article:

When you're working with a diverse group of colleagues and competitors, you have a built-in system of checks and balances. You always have someone asking tough questions at lab meeting or looking over your shoulder to make sure you're doing solid work, with a solid methodology. 

With an increasingly liberal body of professors, institutionalized disconfirmation breaks down. (Not because conservatives are better researchers than liberals, but because of the whole 70:1 ratio thing.) Bad research gets funded. Bad ideas get published -- and this is devastating. 

Why? Because a single bad paper -- even after multiple retractions, and hundreds of studies disproving the bad study's findings -- can influence public's beliefs for decades. Consider the whole anti-vaxxer movement. People wrongfully believe that vaccines cause autism, because a single fraudelent paper written by Andrew Wakefield in 1998. Wakefield had several undeclared conflicts of interested, manipulated his data, and broke several other ethical codes.

Yet here we are in 2016. Within the scientific comunity, the paper has been thoroughly debunked... yet people are still citing Wakefield as a reason to put their children at risk for disfiguring, crippling, fatal, and completely preventable childhood diseases. ​Read more >
​

​This is why scientists and mathematicians don't publish papers without having peers review their work. One small mistake could result in decades of fear mongering and misinformation. 

And it's not as though science reporting is helping. In case you missed John Oliver's amazing take on this:

I even had a student successfully apply to Stanford this year with an essay about science writing, because his message was to important and compelling to ignore. 

Not only that, though: the Wall Street Journal recently published Exclusive Test Data: Many Colleges Fail to Improve Critical Thinking Skills. This analysis found that at least a third of college seniors were unable to make a cohesive argument, assess the quality of evidence in a document or interpret data in a table.

For the sake of being a "good" scientific reporter, I'll point out a few important details, here: 

• Measuring critical thinking is hard. Measuring any kind of intelligence is hard. It's important to be skeptical of any measure of intelligence. The strength of this test, the Collegiate Learning Assessment Test (CLA+), is that it doesn't measure knowledge, but the ability to manipulate information, make inferences, and distinguish valid from flawed information. It is administered to freshmen and seniors. In this analysis, the scores were averaged, then researchers looked at the delta to see added value for critical thinking kills. 
• The CLA+ is for internal use only at public and private universities -- it's used to get accredited. Meaning that students weren't necessarily motivated to perform their best on this test. The schools benefit. The students ​do not. (Even so, the motivation level should be the same whether students are freshmen or seniors, and this analysis was looking at progress and improvement, so it shouldn't terribly matter -- the effect should cancel out with a large enough sample size.)
• The data came from a public information request, meaning that only public schools were measured. (However, because the data compared improvement of students within the same university, each school set its own benchmark.)
• Quite frankly, we don't know how much of this the colleges' fault, versus internships, work experiences, semesters abroad, and other components of a young person's intellectual development. A lot happens between the ages of 18 and 22. 

Correspondingly, employers have begun complaining that new graduates are not ready for the workplace -- and the number one reasons are below proficient critical thinking and writing skills.

THAT IS WHY I force my students to prove that 1 + 1 = 1. THAT IS WHY I often ask them to write the same paper twice -- but arguing opposite perspectives. THAT IS WHY I believe that if a student is going to read ONE book before starting college, it should be The Righteous Mind: Why Good People are Divided by Politics and Religion, by moral psychologist and New York University Stern School of Business Professor Jonathan Haidt.

Students need to learn critical thinking skills. They need to learn how to tell which information is true, and which methodologies are bunk. They need to learn how to adopt a perspective other than their own. They need to learn about logical fallacies, such as the Red Herring, the Straw Man, ad hominems (Hi, Evergreen State College!), the availability heuristic, and the confirmation bias. 

Honestly, I would even be in favor of getting rid of Calculus and focusing ruthlessly on Statistics, which is much more useful to a much larger proportion of students. But that's a story for another day. 

​Not only because it is one of the best ways to stand out to teachers, professors, and hiring managers. 

Not only because it will prevent dangerous or hasty policies.

But because the quest for truth depends on it. 

***

Want to learn more? Check out: 

• Going to Stanford Doesn't Mean You'll Get a Stanford Education.
• If You Want to be Pre-Med, READ THIS.
• APs Make You Look Complacent, NOT Curious.
• Half of America's Top Students Do the Same Six Jobs After Graduation. The Reason Why is Depressing.